Sorting Algorithm - Merge Sort

Merge Sort is a comparison algorithm that tries to sort the dataset by a Divide And Conquer method. The performance of this algorithm is $O(n*log(n))$.

How

We start by splitting the array up into separate elements, then we start by merging pairs together and we make sure that the smallest element is always on the left (this makes sure that our first index on the end is correct too). If the array start getting bigger then 2 elements, then we join those larger arrays by going through their elements one by one and putting the smallest one first.

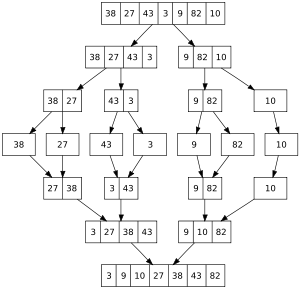
For the implementation check paragraph §5.4.

Advantages and Disadvantages

Advantages

• Stable
• $\Theta(n*lg(n))$ Performance
• Doesn't need random access to data

Disadvantages

• Not adaptive
• $\Theta(n)$ extra space normal
• $\Theta(lg(n))$ Extra space for LinkedLists

Performance

|Worst Case|Average Case|Best Case| |-|-|-| |O(n log n)|O(n log n)|O(n log n)|

For the performance of merge sort we will go out from the assumption that $n = 2^k$. This is because we can then split the table in 2 every time.

$T(n) = 2T(n / 2) + cn$

cn stands for the number of operations needed for merging. This is because merging 2 sub tables is $\Theta(n1 + n2)$. Now to solve this equation we will just divide both terms by n.

$$\frac{T(n)}{n} = \frac{T(n / 2)}{n / 2} + c$$

And we keep on doing this (recursion) because we need the table to become 1 element big.

$$\frac{T(n/2)}{n/2} = \frac{T(n / 4)}{n / 4} + c$$ $$\frac{T(n/4)}{n/4} = \frac{T(n / 8)}{n / 8} + c$$ $$\frac{T(2)}{2} = \frac{T(1)}{1} + c$$

On the end we just add them both together and we get:

$$\frac{T(n)}{n} = T(1) + ck$$

Because $$T(1)$$ is a constant we can say that $T(n) = O(n*lg(n))$. Also when n is not a power of 2, then we get the same result.

Implementation

Implementing this algorithm is not so hard if you know how to, you need to keep 2 methods in mind:

• Merge (Combines 2 arrays with each other)
• MergeSort (Main method, accepts a dataset, splits it and calls this method for those 2 splitted parts)

Then just recursively call MergeSort and you are done.

C++ Code

void merge(vector &v, const vector &left, const vector &right) const {
  // We will save our merged array here
  vector result;

  // Create indexes for the 2 arrays
  int idxLeft = 0;
  int idxRight = 0;

  // Make sure we are not at the end of one of the arrays, else we can't compare
  while (idxLeft < left.size() && idxRight < right.size()) {
    if (left[idxLeft] < right[idxRight]) {
      result.push_back(left[idxLeft]);
      idxLeft++;
    } else {
      result.push_back(right[idxRight]);
      idxRight++;
    }
  }

  // Add remaining elements
  while (idxLeft < left.size()) {
    result.push_back(left[idxLeft]);
    idxLeft++;
  }

  while (idxRight < right.size()) {
    result.push_back(right[idxRight]);
    idxRight++;
  }

  // Set our vector on the result
  v = result;
};

void merge_sort(vector &v) const {
  // Stop running recursively once we have 1 element!
  if (v.size() == 1) {
    return;
  }

  // Find the middle element
  vector::iterator middle = v.begin() + (v.size() / 2);

  // Create our 2 sub arrays
  vector left(v.begin(), middle);
  vector right(middle, v.end());

  // Recursively call MergeSort again, needed for the left and right
  merge_sort(left);
  merge_sort(right);

  // Merge the left and the right array
  merge(v, left, right);
}

1.5.5. Benchmark

| | 100 | 1.000 | 10.000 | 100.000 | 1.000.000 |-|-|-|-|-|-| |Random Elements|0.000163|0.001637|0.018098|0.19313|2.01314 |Ascending Elements|0.000145|0.001474|0.016712|0.172718|1.85952 |Descending Elements|0.00015|0.001472|0.016825|0.173975|1.84874

1.5.6. Conclusion

When sorting a Linked List Mergesort is the best choice, however for normal arrays it is better to use other algorithms such as heap sort (which requires less space) or quicksort.