Heap Sort

Heap sort works by using the heap datastructure. This sorting algorithm has a performance of $O(n*log(n))$ which makes it fast.

How

Heapsort works by first creating the heap datastructure, so let's say we have an array, it will then convert this array into a heap datastructure which is a tree from top to bottom from left to right with our elements.

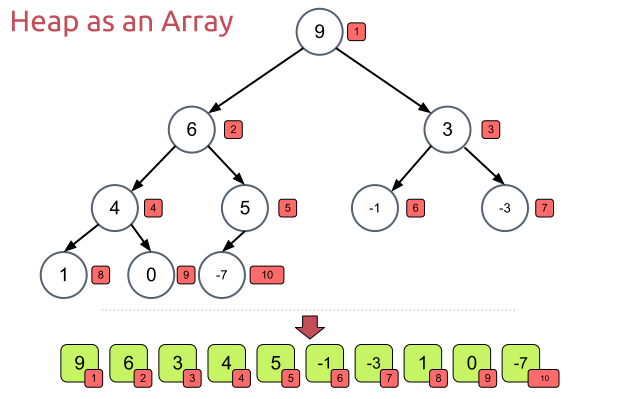
After it has done that it will start executing the Heapify algorithm, heapify works by starting on the second last row of our tree and then comparing the 2 childs, if one of the childs is bigger then the parent, then we swap those 2 and we start heapify again from the swapped child.

Once we are done using the recursive Heapify, we get a sorted array!

For the implementation check paragraph §4.4.

Credits to Stoimen for the graphics.

Advantages and Disadvantages

Advantages

• $O(1)$ extra space
• $O(n*lg(n))$ performance

Disadvantages

• Can be hard to implement if you do not understand it completely.
• Not stable
• Not adaptive

Performance Full Binary Tree

|Worst Case|Average Case|Best Case| |-|-|-| |O(n log n)|O(n log n)|O(n log n)|

Worst Case

For the worst case we will act as if we fill the tree. This will give us an execution time of:

$$ T(n) \leq 2 * 1 + 4 * 2 + 8 * 3 + … + 2^{h-2}(h-2) + 2^{h-1}(h-1) + 2^hh $$

Which we can solve by multiplying both terms by a factor 2.

$$ 2T(n) \leq 4 * 1 + 8 * 2 + 16 * 3 + … + 2^{h-1}(h-2) + 2^h(h-1) + 2^{h + 1}h $$

And then we substract both those equations from one another.

$$ T(n) \leq - 2 - 4 - 8 - 16 - … - 2^{h-1}-2^h+2^{h+1}h $$

Which we can simplify to:

$$ T(n) \leq 1 - (1 + 2 + 4 + 8 + … + 2^h) + 2^{h+1}h $$

This in turn is a serie which we can shorten down:

$$ T(n) \leq 2 + 2^{h+1}(h-1) $$

Since $2^h \leq n \le 2^{h+1}$ we get that:

$$T(n) \leq 2n lg(n) + 2$$

which results into a $O(n*lg(n))$ algorithm in the worst case.

Note that the performance is the same for all the trees, we will always have to go down and keep repeating this n log n times no matter what.

Implementation

The way I started on implementing this algorithm is by drawing it out on a paper step by step, variable by variable.

Once you do that you can see that the trick is to have some sub-methods and finding the correct indexes for this method. By this I found that my methods were:

• getChildLeftIndex // $2 * idxEl + 1$, converted into (index < < 1) + 1
• getChildRightIndex // $2 * (idxEl + 1)$, converted into (index + 1) < < 1
• getHeightTree // $log_2 (elCount + 1) - 1$, log is heavy so I wrote a shifter till we get this.
• getSecondLastHeightStartIndex // Calculate the second last height starting index, this is just $(2^h - 1) - 1$
• buildMaxHeap
• maxHeapify

C++ Code

/**
* ChildLeft = 2 * idx_el + 1
*/
int getChildLeftIndex(int index) const {
  //return 2 * index + 1;
  return (index << 1) + 1;
}

/**
* ChildRight = 2 * (idx_el + 1)
*/
int getChildRightIndex(int index) const {
  //return 2 * (index + 1);
  return (index + 1) << 1;
}

/**
* GetHeightTree(arraySize) = shiftLeft starting from 1 as long as < arraySize (log base 2 of (elCount + 1) - 1)
*/
int getHeightTree(int arraySize) const {
  int i = 1;
  int height = 0;

  while (i < arraySize) {
    i <<= 1;
    height++;
  } 

  return height - 1; // -1 don't include root element 
} 

/** 
 * GetSecondLastHeightStart() = (2^h - 1) - 1 ==> 
 *     last -1 since we want to rebase to 0 for array index
 */
int getSecondLastHeightStartIndex(int h) const {
  // Simulate 2^h
  int i = 1;
  int value = 1;

  while (i <= h) {
    value <<= 1;
    i++;
  }

  return value - 2;
}

void buildMaxHeap(vector &v) const {
  for (int i = (int)floor(v.size() / 2); i >= 0; i--)
    maxHeapify(v, i, v.size());
}

/**
* endIndex and startIndex are here so that we can sort in array
*/
void maxHeapify(vector &v, int i, int endIndex) const {
  int elLeftIndex = getChildLeftIndex(i);
  int elRightIndex = getChildRightIndex(i);

  // Put biggest node on root
  int largestNodeIdx = i;

  // If left child is the biggest, replace with parent
  if ((elLeftIndex < endIndex) && (v[largestNodeIdx] < v[elLeftIndex])) {
    largestNodeIdx = elLeftIndex;
  }

  // if right child exists, check if it is less than
  if ((elRightIndex < endIndex) && (v[largestNodeIdx] < v[elRightIndex])) {
    largestNodeIdx = elRightIndex;
  }

  // If one of the 2 was larger than the parent
  if (largestNodeIdx != i) {
    // Switch parent with child
    int temp = v[i];
    v[i] = v[largestNodeIdx];
    v[largestNodeIdx] = temp;

    // ReApply maxHeapify on the subtree
    maxHeapify(v, largestNodeIdx, endIndex);
  }
}

void heapSort(vector &v) {
  int heapSize = v.size();

  // Eerst heapify
  buildMaxHeap(v);

  // Nu sortdown, hier gaan we telkens het eerst el nemen en vervangen met het laatste el, Hierna resizen we de array en repeat
  for (int i = v.size() - 1; i > 0; i--) {
    // Swap eerste en laatste
    T tmp = v[0];
    v[0] = v[i];
    v[i] = tmp;

    // Maak de heap opnieuw
    maxHeapify(v, 0, i);
  }
}

Benchmark

| | 100 | 1.000 | 10.000 | 100.000 | 1.000.000 |-|-|-|-|-|-| |Random Elements|1.7e-05|0.000303|0.003413|0.041913|0.511796 |Ascending Elements|1.7e-05|0.000279|0.003012|0.036692|0.433318 |Descending Elements|1.5e-05|0.000268|0.002758|0.035744|0.413004

Conclusion

Heap sort is a fast algorithm that you should use if you know how to implement it.