Quantum Computing - An Introduction

Quantum Computing is a hype growing more and more these days, but what is it? Why should we use it and how can we get started with it? This is what I would like to tackle in this post.
Quantum Computing?
As written in the excellent publication by Richard P. Feynman - Simulating Physics with Computers, we would like to have a kind of computer that does exactly the same as nature. A computer that is able to simulate the real world better, and next to that allows us to tackle larger and more complex problems. Think for example about problems such as:
- Quantum Chemistry
- Quantum Dynamics
- Material Science
- Optimization Problems
- Sampling
- Secure Computing
- Cryptography
- Machine Learning
- Searching
To solve these kind of problems, we need to fundamentally change computers as they work now, transforming from classical bits towards qubits. However before we get started, I recommend you to take a refresher of Linear Algebra to have the fundamentals needed to continue :)
Qubits?
Introduction
Now what are Qubits? When we look at nature, it does not represent everything binary as we do now, take a look at these examples:
- An electron can be in spin up or spin down
- A photon can have a vertical or horizontal polarization
All these kind of examples can be represented as a qubit, representing a 2-state quantum mechanical system.
How does an electron look with its spins?
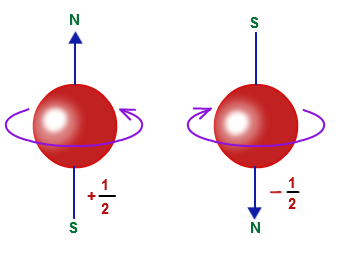
There are 2 main aspects in Quantum Physics:
- Entanglement: Particles can become connected so that we can predict the state of the other (e.g. one elctron is spin-up, then we know the other is spin-down if they are entangled)
- Superposition: A quantum system can be in multiple states at the same time until it is measured
Mathmatical Representation
Of course to be useful in Quantum Computing, we need to represent these qubits in a mathmatical way. This we can by using the "ket" notation of before, representing a qubit as:
$$ \vert \psi \rangle = \alpha \vert 0 \rangle + \beta \vert 1 \rangle = \alpha * \begin{bmatrix} 1 \ 0 \end{bmatrix}
- \beta * \begin{bmatrix} 0 \ 1 \end{bmatrix} $$
With $\alpha$ and $\beta$ being probability amplitudes (describes the behaviour of the system), with extra constraint that $\vert \alpha \vert^2 + \vert \beta \vert^2 = 1$
Seeing that we are working with a 2-level system that uses complex numbers, we can thus represent this on a sphere called the Bloch Sphere:
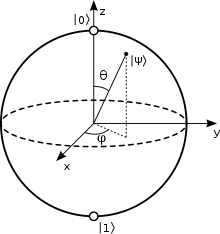
Where the angles are described by: $\alpha = cos(\frac{\theta}{2})$ and $\beta = e^{i * \theta} * sin(\frac{\theta}{2})$
Using Quantum Circuits to create Quantum Algorithms
Introduction
To start working with Quantum Computing, we create circuits by using quantum gates. A good overview of the different gates can be found on Wikipedia, so I will not go too much on depth on these. These Quantum Gates are the building blocks of circuits and allow us to write our different programs and algorithms.
A mathmatical example
Let's actually calculate an example. When we for example combine a hadamard gate with a CNOT gate:
The Hadamard Gate is called the "Fair Coin Flip", inducing an equal probability of the qubit being in either of the states
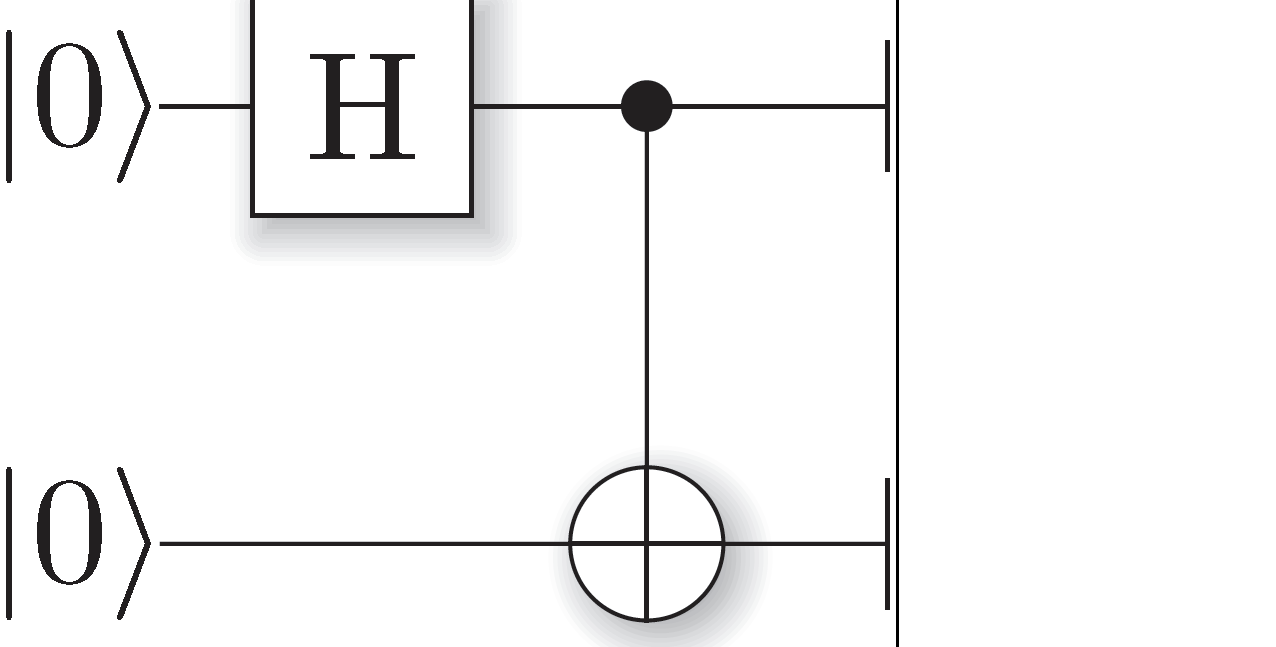
Then we know the following:
(Define Psi, Theta, Hadamard, Identity and CNOT)
$$ \vert \psi \rangle = \begin{bmatrix} \alpha \ \beta \end{bmatrix} ; \vert \theta \rangle = \begin{bmatrix} \gamma \ \delta \end{bmatrix} ;
H
\frac{1}{\sqrt(2)} * \begin{bmatrix} 1 & 1 \ 1 & -1 \end{bmatrix} ;
I
\begin{bmatrix} 1 & 0 \ 0 & 1 \end{bmatrix} ;
CNOT
\begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 1 \ 0 & 0 & 1 & 0 \end{bmatrix} $$
Which we can work out for 2 cross products already (Psi and Gamma; Hadamard and Identity):
(Work out Cross Product of Psi and Gamma, Hadamard and Identity)
$$ \vert \psi \rangle \otimes
\vert \theta \rangle
\begin{bmatrix} \alpha \gamma \ \alpha \delta \ \beta \gamma \ \beta \delta \end{bmatrix} ;
H \otimes I
\frac{1}{\sqrt(2)} * \begin{bmatrix} 1 & 1 \ 1 & -1 \end{bmatrix} * \begin{bmatrix} 1 & 0 \ 0 & 1
\end{bmatrix}
\frac{1}{\sqrt(2)} * \begin{bmatrix} 1 & 0 & 1 & 0 \ 0 & 1 & 0 & 1 \ 1 & 0 & -1 & 0 \ 0 & 1 & 0 & -1 \end{bmatrix} $$
Resulting in:
$$
CNOT * (H \otimes I) * (\vert \psi \rangle \otimes \vert \theta \rangle)
\begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 1 \ 0 & 0 & 1 & 0 \end{bmatrix} \frac{1}{\sqrt(2)} * \begin{bmatrix} 1 & 0 & 1 & 0 \ 0 & 1 & 0 & 1 \ 1 & 0 & -1 & 0 \ 0 & 1 & 0 & -1 \end{bmatrix} \begin{bmatrix} \alpha \gamma \ \alpha \delta \ \beta \gamma \ \beta \delta \end{bmatrix}
\
\frac{1}{\sqrt(2)} * \begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 1 \ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} \alpha \gamma + \beta \gamma \ \alpha \delta + \beta \delta \ \beta \gamma - \beta \gamma \ \beta \delta - \beta \delta
\end{bmatrix}
\frac{1}{\sqrt(2)} * \begin{bmatrix} \alpha \gamma + \beta \gamma \ \alpha \delta + \beta \delta \ \alpha \delta - \beta \delta \ \alpha \gamma - \beta \gamma \end{bmatrix} $$
Quantum Algorithms
Interesting Quantum Algorithms are:
- Grover Search: Find an element in an unordered array. Worse case using Quantum here is $\sqrt(n)$ which is normally N using convential algorithms.
- Short's Factoring: Factor an integer in its prime factors. With Quantum this is possible in Polynomial time (RSA encryption is based on Prime Factors, showing the impact quantum can have here)
For an implementation of these algorithms, feel free to check this awesome article



Comments ()