Introduction to Algorithms

In the last semester of school we are learning about datastructures and algorithms. Because this is a very popular subject for companies, I have decided to write articles about it. They will be numbered from easy to hard so that you are able to learn the most critical sorting algorithms first. Also please note that all the code written here has been written by my (unless specified otherwise), because of this there might be some bugs, please contact me if you find any.
Analysing Algorithms
To compare algorithms, we look at the worst case, theaverage case and the best case. These are the cases that will impact our running time the most. For most algorithms, we do know the formulas to describe these cases, while there are others which we don't understand at all.
When we start analysing, we will see that it is impossible to get an exact timing for the performance of all algorithms, this is because there are a lot of factors that we have to calculate in such as the compiler being used, the programming language, the cpu, …
Therefor when we analyse an algorithm, we try to find a collection of primitive operations. These primitive operations allow us to find an abstract model that will work on any implementation.
Asymptotic Notations
O Notation
Formal method for expressing the upper bound of an algorithm's running time. It measures the longest time an algorithm takes to complete.
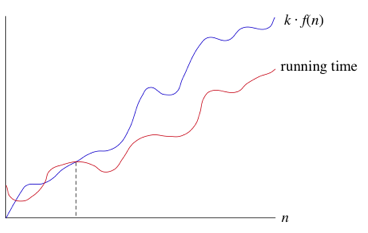
"If a running time is $O(f(n))$, then for large enough $n$, the running time is at most $k * f(n)$ for some const $k$. Here's how to think of a running time that is $O(f(n))$" 1.:
Ω Notation
When we want to say an Algorithm takes at least a certain amount of time, then we use the Omega Notation.
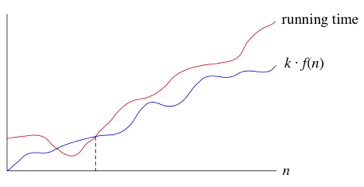
"if a running time is $\Omega(f(n))$, then for large enough $n$, the running time is at least $k * f(n)$ for some constant $k$. Here's how to think of a running time that is $\Omega(f(n))$" 1.:
Θ Notation
The Theta Notation gives us the worst-case running time of an algorithm.
"When we say that a particular running time is $\Theta(n)$, we're saying that once $n$ gets large enough, the running time is at least $k1 * n$ and at most $k2 * n$ for some constants $k1$ and $k2$. Here's how to think of $\Theta(n)$" 1.:

Benchmarking Algorithms
To benchmark algorithms, I use a specific framework that was given to us by our professors. We had to complete this code ourselves so that we were able to easily add algorithms and get a benchmark out of them. (Credits for this code towards my professors and me).
main.cpp
#include
#include /* srand, rand */
#include /* time */
#include "sortvector.h"
#include "sortmethod.h"
#include "chrono.h"
int main() {
srand(time(NULL)); // seed it
HeapSort is;
meet(1, 6, is, std::cout);
return 0;
}
chrono.h
#ifndef Labo2_chrono_h
#define Labo2_chrono_h
#include
class Chrono{
public:
Chrono();
void start();
void stop();
double tijd() const;
private:
clock_t start, end;
};
Chrono::Chrono(){}
void Chrono::start(){
start = clock();
}
void Chrono::stop(){
end = clock();
}
double Chrono::tijd() const{
return static_cast(end - start) / CLOCKS_PER_SEC;
}
#endif
sortmethod.h
#ifndef Labo2_sortmethod_h
#define Labo2_sortmethod_h
#include
using std::endl;
using std::cout;
#include
using std::vector;
#include // voor sort()-methode uit STL
#include // setw()
#include // floor
template
class Sortmethod{
public:
virtual void operator()(vector & v) const = 0;
};
/*
* STANDARD TEMPLATE LIBRARY SORT
*/
template
class STLSort : public Sortmethod{
public:
void operator()(vector & v) const;
};
template
void STLSort::operator()(vector & v) const{
sort(v.begin(),v.end());
}
/*
* MERGE SORT : Not implemented
*/
template
class MergeSort : public Sortmethod {
public:
void operator()(vector & v) const;
};
template
void MergeSort::operator()(vector &v) const {
};
#endif
sortvector.h
#ifndef Labo2_sortvector_h
#define Labo2_sortvector_h
// sortvector is een klasse van sorteerbare vectoren
#include
using std::istream;
using std::ostream;
#include // voor setw
#include // voor rand - opletten!!
#include "sorteermethode.h"
#include "chrono.h"
#include "csv.h"
#include "Nstring.h"
template
class Sortvector{
public:
Sortvector(int);
Sortvector(const Sortvector& v) = delete;
Sortvector& operator=(const Sortvector& v) = delete;
Sortvector& operator=(Sortvector&& v) = delete;
Sortvector(Sortvector&& v) = delete;
const T &operator[](int i) const { return tab[i]; }
T &operator[](int i) { return tab[i]; }
void sorteer(const Sorteermethode & methode);
void vul_range();
void draai_om();
void vul_omgekeerd();
void shuffle();
void vul_random_zonder_dubbels();
void vul_random(); // nog niet implementeren
bool is_gesorteerd() const;
bool is_range() const;
friend ostream& operator<<(ostream& os, const Sortvector& s){
s.schrijf(os);
return os;
}
private:
vector tab;
void schrijf(ostream & os)const;
int n; // Aantal elementen
};
template
void Sortvector::schrijf(ostream & os)const{
for(int i=0; i<tab.size(); i++){
os<<tab[i]<<" ";
}
os<<endl;
}
template
Sortvector::Sortvector(int elementCount) {
n = elementCount;
}
template
void Sortvector::vul_range() {
for (int i = 0; i < n; i++) {
tab.push_back(i);
}
}
template
void Sortvector::draai_om() {
std::reverse(tab.begin(),tab.end());
}
template
void Sortvector::vul_omgekeerd() {
for (int i = n - 1; i >= 0; i--) {
tab.push_back(i);
}
}
template
void Sortvector::sorteer(const Sorteermethode & methode) {
methode(tab);
}
template
void Sortvector::shuffle() {
int n = tab.size();
for (int i = n - 1; i > 0; --i) {
std::swap(tab[i], tab[rand() % (i + 1)]);
}
}
template
void Sortvector::vul_random_zonder_dubbels() {
vul_range();
shuffle();
}
template
bool Sortvector::is_gesorteerd() const {
for (int i = 1; i < n; i++) { if (tab[i - 1] >= tab[i]) {
return false;
}
}
return true;
}
template
bool Sortvector::is_range() const {
for (int i = 0; i < n; i++) {
if (tab[i] != i) {
return false;
}
}
return true;
}
template
void meet(int kortste, int langste, const Sorteermethode & sm, ostream& os) {
int lengte = kortste;
// Print header
os << std::setw(10) << "Lengte\t\t"
<< "random\t"
<< "gesorteerd\t"
<< " omgekeerd"
<< std::endl;
// Print results
for (int i = 0; i < langste; i++) {
lengte *= 10;
Sortvector svr(lengte);
svr.vul_random_zonder_dubbels();
Sortvector svg(lengte);
svg.vul_range();
Sortvector svo(lengte);
svo.vul_omgekeerd();
Chrono cr;
cr.start();
svr.sorteer(sm);
cr.stop();
Chrono cr2;
cr2.start();
svg.sorteer(sm);
cr2.stop();
Chrono cr3;
cr3.start();
svo.sorteer(sm);
cr3.stop();
os << std::setw(10) << lengte
<< "\t" << std::setw(10) << cr.tijd()
<< "\t" << std::setw(10) << cr2.tijd()
<< "\t" << std::setw(10) << cr3.tijd()
<< std::endl; } } #endif
For the full code with comments, please go check out my Github
References
To create all these articles I have used several resources on the internet, in books, and in our text book gotten from school.
- Sedgewick, Robert. Algorithms in C++, Parts 1-4: Fundamentals, Data Structure, Sorting, Searching, Third Edition Addison-Wesley, 1998.
- Stoop, Rudy and Cnops, Jan. Course Datastructures and Algorithms Textbook University Ghent, 2015
- Asymptotic Notation, https://www.khanacademy.org/computing/computer-science/algorithms/asymptotic-notation, 15 March 2015 (1.)
- Shellsort, http://nl.wikipedia.org/wiki/Shellsort, 15 March 2015
- Selection Sort, http://en.wikipedia.org/wiki/Selection_sort, 15 March 2015
- Heap Sort, http://en.wikipedia.org/wiki/Heapsort, 15 march 2015
- Heap Sort, http://www.stoimen.com/blog/2012/08/07/computer-algorithms-heap-and-heapsort-data-structure/, 15 march 2015
- Merge Sort, http://en.wikipedia.org/wiki/Merge_sort, 15 march 2015
- Vladimir Yaroslavskiy, Dual-Pivot Quicksort, http://iaroslavski.narod.ru/quicksort/DualPivotQuicksort.pdf, 16 March 2015
- Sebastian Wild, Markus E. Nebel, Conrado Martínez, Analysis of Dual Pivot Quicksort, http://arxiv.org/pdf/1412.0193v1.pdf, 16 march 2015



Comments ()